ゆるふわリー群論入門（３）多様体

この記事は、リー群と表現のざっくりふんわりとした解説記事の3本目です。

前回：線形リー群
cake-by-the-river.hatenablog.jp

今回は、多様体という観点を導入します。

多様体的アプローチ

前回は、リー群を線形リー群などに局所同型な位相群として定義しました。そこで、リー群における「局所」の具体的なイメージを考えて行くことにしましょう。

接平面

2次の特殊線形群 $SL(2, \mathbb{R})$ を考えます。この行列を4次元のベクトルと捉えなおすことで、相対位相が導入できました。 $SL(2, \mathbb{R})$ は、4次元空間 $\mathbb{R}^4$ での $x = (x_1, x_2, x_3, x_4)$ という座標系を考えたとき、

$det(x) = x_1 x_4 - x_2 x_3 = 1$

という方程式を満たす超曲面にあたります。3次元空間において1つの方程式で表される図形が（2次元的な）曲面に対応する様子を、さらに高次元である場合でも同じように考えた名称が超曲面です。ここからは、どうしても4次元を図にすることは出来ないため、3次元的な図に合わせて4次元やもっと高次元の世界を何となく想像するようにしてください。

$SL(2, \mathbb{R})$ は単位元を含んだ超平面ですが、単位元付近（単位元近傍）の $SL(2, \mathbb{R})$ の（ベクトル化した）点についてみていきます。例えば、単位元 $E = (1, 0, 0, 1)$ から少しだけズレた点 $x(t) = (1+t, 0, 0, \frac{1}{1+t})$ も、 $SL(2, \mathbb{R})$ に含まれていることが分かりますね。この点 $x(t)$ のパラメータ $t$ を限りなく 0 まで近づけていくと、急激な変化なく穏やかに単位元へと移っていく感じがします。

この「穏やかに」というのは、パラメータ $t$ で表される曲線に対して単位元で”接線”がきれいに引けそう！と言い換えられそうです。実際、

$\displaystyle \overrightarrow{X} = \lim_{t\to0}\frac{x(t) - E}{t} = (1, 0, 0, -1)$

と”接ベクトル”が求まるので、確かにこの曲線上を穏やかに通り過ぎることが分かります。もし接ベクトルが定まらないときは、その点で曲線が折れ曲がっているのだろうと言えます。

f:id:cakkby6:20200225000758p:plain — 本来は4次元空間です

実を言うと、単位元を通る他のどんな曲線においても、きれいに接線が引けます。つまり、単位元における接平面（この場合は3次元なので、むしろ「接超平面」）が存在しています。曲面上のどんな曲線も接線を持つというのは、単位元の微小な近傍においては曲線をほぼ直線と捉えても良いことになります。そして、それら全ての直線の集合、つまり接ベクトルの集合は接平面を構成するのだと言えます。

さらに、 $SL(2, \mathbb{R})$ 上のどの点においても接平面の存在が言えます。これは、どの点の勾配 $grad$ も計算上は零ベクトルにならないからです。 $\boldsymbol{x} \in SL(2, \mathbb{R})$ の方程式 $F(\boldsymbol{x}) = 0$ において、 $grad$ は接平面の方程式を決定します。つまり、 $F(\boldsymbol{x}') = 0$ なる点 $\boldsymbol{x}'$ で

$(grad F)(\boldsymbol{x}') \cdot (\boldsymbol{x} - \boldsymbol{x}') = 0$

が接平面の方程式になります。このとき $grad F$ が零ベクトルではない、つまり必ず存在するならば、それに対応した接平面も存在するということです。この結果、 $SL(2, \mathbb{R})$ は至る所でツルツルな図形だと言えます。

f:id:cakkby6:20200225203034p:plain

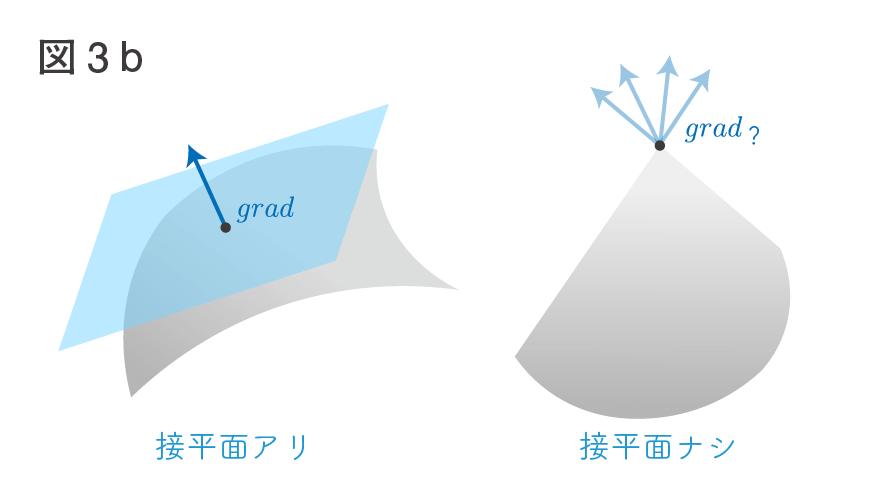
ところで接平面が考えられたのなら、その点の微小な範囲の近傍（ $\varepsilon$ -近傍など）は接平面と似通っていると思いませんか？つまり、リー群の元の微小な近傍の上には接平面的な空間が存在し、それは本体にかなり似た空間を構成しているのでしょう。

そういうことなら、その”接平面”自体をよく調べてみればリー群の性質が詳しく分かるようになるかもしれないですね。実は、この”接平面”にあたるもの（線形空間）はリー環と呼ばれているものになります。ただし、この"接平面"という概念をもっと詳しく考えなければいけないので、リー環についてやる前に、もう少しだけ厳密に”接平面”を知る必要があります。

多様体

（多様体論について分かる人は飛ばしてください）

「滑らかな図形を平面で近似する」と言えば、私たちの住んでいるこの地球でも同様なことが言えます。私たちは、地球が球に近い形であることを知っています。しかし、私たちが普段目にしている空間は地表面の本当にわずかな範囲でしかなく、私たちは地球の丸さを感じるよりも、まるでその接平面の上に立っているような気がします。

そうなると、私たちが住む範囲に独特な「局所座標」を考えるのが自然になります。地球上のわずかな範囲にある物体の動きを見る際に、地球のど真ん中を原点とする3次元空間を考えるようなことはまずありません。地表を平面と近似して考え、局所的な2次元空間を設定して家の座標を決めたりします。地図上で物事を考える方が、宇宙空間を表現する3次元とみて考えるよりも、はるかに分かりやすいからです。

f:id:cakkby6:20200225212730p:plain

これと同じことを数学上でも考えよう！というのが局所座標、また多様体というものになります。次に示す局所座標（系）の定義は一見して分かりにくいですが、下の図と合わせて考えれば分かりやすくなります。

位相空間 $M$ の開集合 $U$ から $\mathbb{R}^m$ の開集合 $U'$ への位相同型写像

$\varphi: U → U'$

が存在する時、 $U$ と $\varphi$ の組 $(U, \varphi)$ を座標近傍、 $\varphi$ を $U$ 上の局所座標系（チャート）という。座標近傍 $(U, \varphi)$ 内の任意の点 $p$ は $\mathbb{R}^m$ の点 $\varphi(p) = (x_1, x_2, \dots, x_m)$ と表せる。これらの座標を、 $p$ の局所座標という。

また、位相空間 $M$ がハウスドルフ空間で、 $M$ 上の任意の点 $p$ に対して、 $p$ を含む座標近傍 $(U, \varphi)$ が存在する時、 $M$ を m次元位相多様体と呼ぶ。位相多様体全体を被覆する座標近傍の全体（集合）は座標近傍系（アトラス）と呼ばれる。

f:id:cakkby6:20200225212818p:plain

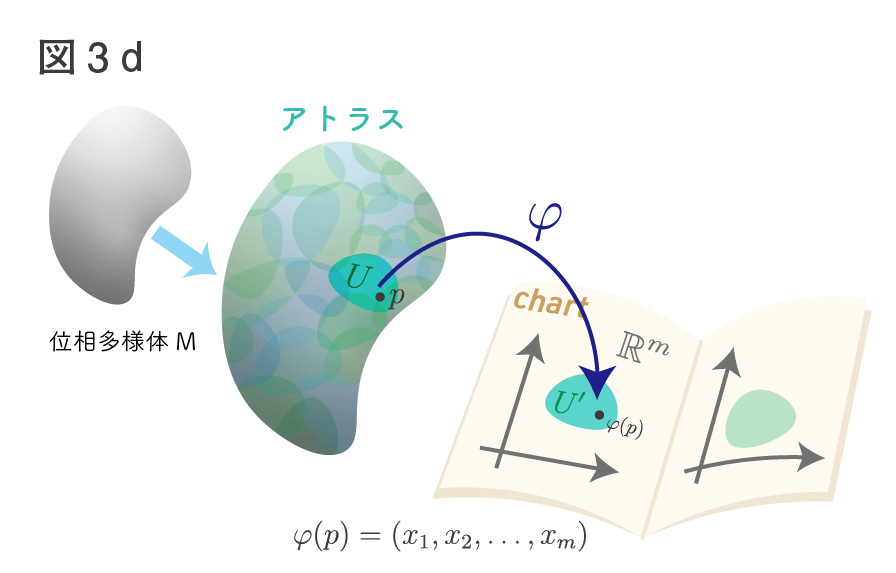
チャートとは地図の事です。ある位相空間の局所的な構造が $\mathbb{R}^m$ と似ていた場合（位相同型な場合）、 $\mathbb{R}^m$ の記載された「地図帳」を用意し、開集合をこの地図帳にどんどん記入していきます。そうやって全体をカバーする地図帳が完成した時、位相空間を（位相）多様体と呼ぶことにしたのですね。アトラスとは地図帳の意味ですが、数学的には多様体上に張りついた開集合の全体を指すようです。

多様体上の点が地図上に移されてきたならば、地図上での座標 $(x_1, x_2, \dots, x_m)$ で点を扱うことが出来るようになります。それが局所座標です。この局所座標（地図上の点）は多様体上の点と対応しているので、多様体上に局所座標を「書き込む」ことも出来ます。いずれにせよ、局所座標は座標近傍だけのものですし、開集合ごとに異なります。

さて、上の定義では位相同形としか言ってなかったので、多様体上で接ベクトルのような微分操作をしたければ、多様体が（偏）微分可能かどうかも考えなきゃいけなくなります。普段の $\mathbb{R}^m$ という空間の関数では、 $C^r$ 級＝ $r$ 階まで偏微分可能、 $C^\omega$ 級 = テイラー展開が可能、といった感じでした。局所座標を導入した今、局所的に多様体上の関数の $C^r$ 級、 $c^\omega$ 級を考えるには次のようにします。

位相多様体 $M$ の座標近傍系を $\mathcal{S} = \{(U_\alpha, \varphi_\alpha)\}_\alpha$ とする。 $U_\alpha \cap U_\beta \neq \emptyset$ な $^\forall \alpha, \beta$ に対し、

$\varphi_\beta \circ \varphi^{-1}_\alpha : \varphi_\alpha (U_\alpha \cap U_\beta) → \varphi_\beta (U_\alpha \cap U_\beta)$

が $C^r$ 級の時、 $M$ は $C^r$ 級多様体と呼ぶ（ $C^\omega$ 級なら解析的多様体）。
$C^r$ 級多様体上の関数 $f : M → \mathbb{R}$ が $C^s$ 級関数（ $s <= r$ ）とは、

$f \circ \varphi^{-1}_\alpha : U'_\alpha → \mathbb{R}$

が $U'_\alpha$ 上の $C^s$ 級関数になることである（ $C^\omega$ 級も同様）。

$C^r$ 級多様体の定義より、まずは $C^s$ 級関数の定義を考えると分かりやすいです。 $f \circ \varphi^{-1}_\alpha$ とは、地図上の $U'_\alpha$ を多様体に戻し、さらに多様体上の関数 $f$ によって実数を受け取る関数になります。これが $C^r$ 級というのはつまり、多様体上の関数を地図上の関数に置きなおしてみた関数の $C^r$ 級を意味します。

f:id:cakkby6:20200226004725p:plain

例えば上の図だと、多様体上に表面温度のようなものがあって、それを関数として考えたときに $f \circ \varphi^{-1}$ がどうなるかを表しています。

一方、多様体の座標近傍には（地図帳が同じ地点を複数のページで重複して表示するように）被っている範囲 $U_\alpha \cap U_\beta$ が存在します。その被っている範囲にて、もし関数の $C^r$ 級という性質が座標近傍間で変わるようなら大変です。 $U_\alpha$ では $C^2$ 級だったのに $U_\beta$ だとただの $C^0$ 級だと言われてしまうと困りますね。そこで、被っている範囲での整合性を保つためにも、 $U_\alpha$ から $U_\beta$ へ処理を移す際は同じ $C^r$ 級であることを保証しよう！という考えが、 $C^r$ 級多様体の定義に反映されています（もちろん解析的多様体も同様）。

f:id:cakkby6:20200226120643p:plain

接ベクトル空間

微分を扱えるようになったので、”接平面”について考えてみましょう。

最初の例では、パラメータ $t$ によって決まる曲線を考えていました。この $t$ を時間とみると、局所座標内のこの曲線は $c(t) = (x_1(t), x_2(t), \dots x_m(t))$ のように座標ごとの関数で表されます。これを例えば $t=0$ で時間微分したものは、 $t=0$ の地点での速度ベクトルです。ただ、その見た目は局所座標に依存しており、

$\displaystyle \left( \frac{\mathrm{d}x_1}{\mathrm{d}t}(0), \frac{\mathrm{d}x_2}{\mathrm{d}t}(0), \dots , \frac{\mathrm{d}x_m}{\mathrm{d}t}(0) \right)$

などと書かれます。このままでは、座標近傍に固有な局所座標ごとに、あるいは異なるアトラスごとに異なった表示となってしまいます。まあそれでも良いっちゃ良いかもしれないですが、その座標近傍だけに話を制限したくないこともあるかもしれないので、できれば座標近傍に依存しない要素を取り出してみたいですね。

f:id:cakkby6:20200227232730p:plain

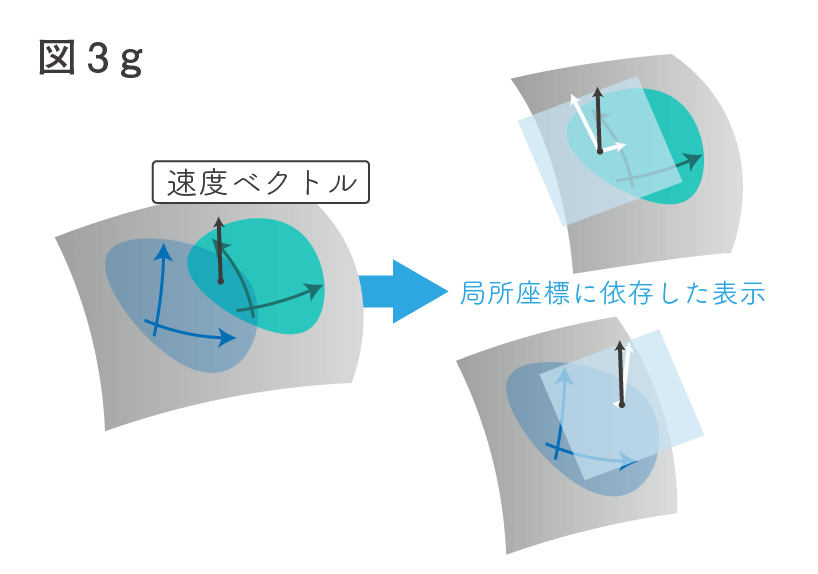
そこで、多様体上の関数 $f$ における勾配ベクトルを利用することにします。なぜなら、関数を介して考えれば局所座標系に依らなくても済むからです。つまり、曲線 $c(t)$ 上での関数 $f$ は

$f(c(t)) = f(x_1(t), x_2(t), \dots x_m(t))$

となりますが、これは結局 $x_i$ といった局所座標系を無視して、 $t$ のみに依存する関数 $f(t)$ だと考えられるからです！

それを時間微分したものは（合成関数の微分法則＝連鎖律によって）

$\displaystyle \frac{\mathrm{d}f(c(t))}{\mathrm{d}t}(0) = \frac{\partial f}{\partial x_1}\frac{\mathrm{d}x_1}{\mathrm{d}t}(0) + \dots + \frac{\partial f}{\partial x_m}\frac{\mathrm{d} x_m}{\mathrm{d} t}(0)$

と書けます。これは、勾配ベクトル（ $grad f = \nabla f$ ）と

$\displaystyle \frac{\mathrm{d} \boldsymbol{x}}{\mathrm{d} t}(0) = \left( \frac{\mathrm{d}x_1}{\mathrm{d}t}(0), \frac{\mathrm{d}x_2}{\mathrm{d}t}(0), \dots , \frac{\mathrm{d}x_m}{\mathrm{d}t}(0) \right)$

によって

$\displaystyle \frac{\mathrm{d}}{\mathrm{d}t} f(0) = \frac{\mathrm{d} \boldsymbol{x}}{\mathrm{d} t}(0) \cdot \nabla f$

と簡潔に表せます。この時、

$\displaystyle \nabla = \left( \frac{\partial}{\partial x_1}, \dots ,\frac{\partial}{\partial x_1} \right)$

を「基底ベクトル $\frac{\partial}{\partial x_i}$ のベクトル」と考え、この基底により張られる空間を導入してみましょう。そうすれば、最初の局所座標表示であった速度ベクトルも、（その局所座標による）偏微分を基底とする一つのベクトルだと考えられます。これなら局所座標が色々と変化したところで、「偏微分が基底のベクトル」であることは不変であり、局所座標に依らない表現が出来ます！

そして、速度ベクトルの”方向”に相当する接ベクトルを色々と集めてくることで、（このページ最初での考察のように）”接平面”に値するものが出てきます。それが「偏微分を基底とする線形空間」です。このような、 $\frac{\partial }{\partial x_i}$ を基底とする線形空間のことを、接（ベクトル）空間と呼びます。多様体 $M$ 上の点 $p$ での接空間は $T_p(M)$ と書かれます。結局は接ベクトル全体がなす線形空間と考えれば良さそうです。今までの”接（超）平面”は、接空間の事を言っていたようです。

微分と逆関数定理

接空間は多様体の近傍に「似ている」と言えます。この「似ている」は、さらに「同型」という表現にまで格上げすることが出来ます。それが、逆関数定理と呼ばれる定理になります。ただその前に、異なる多様体の接空間同士の関係について考えることにします。

多様体から実数への関数における $C^r$ 級という概念が導入できたので、同じようにして多様体から多様体への写像の $C^r$ 級という概念も導入できます。つまり、写像を局所座標表示して関数の塊に分解したとき、それらすべての関数が $C^r$ 級ならば写像も $C^r$ 級と呼ぶことにしよう！ということです。もっと正確には、多様体 $M, N$ 間の写像 $f : M → N, p \mapsto f(p)$ を、 $p, f(p)$ まわりの局所座標上での写像に落とし込んで $C^r$ 級かどうかを判定しようということです。

写像 [f: M → N] が全単射で、 $f, f^{-1}$ とも $C^r$ 級だとしたとき、 $f$ は $C^r$ 級微分同相写像と言います。これは、位相同型写像の $C^r$ 級版での拡張だと考えれば良さそうです。つまり、 $C^r$ 級の1対1対応が存在しているため $C^r$ 級の構造が多様体同士で保存されているということです。

実は、WhitneyとGrauertというおっさんたちの功績により、次の定理が成り立つことが判明しています。

定理　H.Whitney(1936)＋H.Grauert(1958)

（ほぼ）任意の $C^1$ 級多様体には、微分同相な $C^r$ 級多様体が存在している（ $1 \le r \le ∞ , \omega$ ）

つまり、リー群を扱っている間は微分可能な関数を大体 $C^\omega$ 級の関数として考えても構わないんです。ありがたい！微分可能がどうのこうのというのはあまり気にしなくてよかったんですね。定理の「ほぼ」とは σコンパクト（＝コンパクト位相空間の可算個の和集合）と呼ばれる性質の仮定ですが、 $\mathbb{R}^n$ が σコンパクトだそうで、リー群を考える上では大体大丈夫でしょう。

さて、（ $C^r$ 級の）写像 $f: M → N$ で結びついた点 $p, f(p)$ が各々に接空間 $T_p(M), T_{f(p)} (N)$ を持っていたとしましょう。このとき写像 $f$ によって接空間はどのように移されるのか、ということには写像 $f$ の「微分 (Differential) 」という用語が充てられています。

写像 $f:M → N, p \mapsto f(p)$ における接空間同士の（線形）写像

$(df)_p : T_p(M) → T_q(N)$
を、写像 $f$ の点 $p$ における微分と呼ぶ。この写像は（線形空間から線形空間への移動なので）行列によって表現されるが、その行列は

$\displaystyle (Jf)_p = \begin{pmatrix} \frac{\partial f_1}{\partial x_1}(p) & \ldots & \frac{\partial f_1}{\partial x_m}(p) \\ \vdots & \ddots & \vdots \\ \frac{\partial f_n}{\partial x_1}(p) & \ldots & \frac{\partial f_n}{\partial x_m}(p) \end{pmatrix}$

と表される。この行列をヤコビ行列と呼ぶ。

f:id:cakkby6:20200227235002p:plain

重積分の変数変換でおなじみのヤコビ行列が出ました。重積分でのヤコビ行列は、変数変換における微小な体積要素（つまり接空間）の変形を表すものでしたね。それを多様体での変数変換、あるいは写像の微分の変形の様子に自然と拡張したものだと言えそうです。重積分の時とは異なり、変化前と変化先とで次元が異なることもあります。

そして、話題にした「微分同相」と「接空間」の関係を記述する定理が、逆関数定理というものです。

逆関数定理
$C^r$ 級写像 $f: M → N, p \mapsto f(p)$ の微分 $(df)_p: T_p(M) → T_{f(p)}(N)$ が全単射の線形写像をなすならば、 $f$ は $p$ のある近傍 $U$ から $f(p)$ のある近傍 $V$ への $C^r$ 級微分同相写像である。

つまり、接空間同士の微分のヤコビ行列が正則である（ヤコビアンが0でない）とき、 $f$ に逆写像が存在してそれも $C^r$ 級だと言える。

長いし勉強不足でよくわかっていないので、定理の証明はしません！（すみません）ただ、接空間として同じようなものになるならそのヤコビ行列は正則になるはずで、正則なら逆行列を考えればそれが実は逆写像に対応してるよ！って感じだと思います。とにかく、接空間が同じようなものだったら、多様体（の近傍）同士の微分同相であることが言えちゃうということです。これは接平面が多様体自身に「似ている」ことのより正確な表現になります。

この定理の逆、つまり「微分同相なら接空間が同型」というのも成り立ちます（合成写像の微分を考えるそうです）。結果として、

微分 $(df)_p$ が全単射　⇔　 $f$ が $p$ の近傍で $C^∞$ 級微分同相