数理生物学に入門してみる（２）入出力

　今回は教科書の第2章、授業では2~4回目で扱った入出力のモデルについてまとめます。化学反応速度論から初めてフィードフォワードなどの回路の話までやります。

前回

cake-by-the-river.hatenablog.jp

入出力の基本の式
- 結合と解離・Hillの式
- ミカエリス-メンテンの式
Ultrasensitivity
入出力と回路
補足（末尾）
- MWCモデルがシグモイド的になるための条件
- push-pull型反応の解

入出力の基本の式

　前回の”トグル・スイッチ”の例では、タンパク質の量の二乗を分母に持つ形で数値的に解析しました。これは、反応速度論によって分子の結合・解離を解析することで、より一般的に考えることが出来ます。

結合と解離・Hillの式

　希釈な溶液で分子 L と R が結合・解離する反応は、化学反応速度速度論の考えを用いて

$\displaystyle L + R \ \overset{k_{on}}{\underset{k_{off}}{\rightleftharpoons}} \ LR$

$\displaystyle \frac{d [LR]}{dt} = k_{on}[L][R] - k_{off}[LR]$

と書けます。定常状態を考えると上式から $[LR]$ の関係式が現れるため、結合した分子 R の割合（占有率） $p$ は

$\displaystyle p = \frac{[LR]}{[R] + [LR]} = \frac{\frac{1}{K_d} [L][R]}{[R] + \frac{1}{K_d} [L][R]} = \frac{[L]}{K_d + [L]}$

と書けます。なお $\displaystyle K_d = \frac{k_{off}}{k_{on}}$ は解離定数です。

　このような結合解離の関係は、より一般に複数の L が結合する反応でも同様に考えられます。すなわち、 n 個の L が結合する反応では

$\displaystyle nL + R \ \overset{k_{on}}{\underset{k_{off}}{\rightleftharpoons}} \ L_nR$

$\displaystyle \frac{d [L_nR]}{dt} = k_{on}[L]^n[R] - k_{off}[L_nR]$

と書けます。先程と同様に定常状態を考えると、占有率 $p$ は

$\displaystyle p = \frac{\frac{1}{K_d} [L]^n[R]}{[R] + \frac{1}{K_d} [L]^n[R]} = \frac{[L]^n}{K_d + [L]^n}$

として求まります。この式は Hillの式 と呼ばれており、n はヒル係数と呼ばれています。 $[L]^n = K_d$ のとき $p = \frac{1}{2}$ となることから、 $K_d$ はどれくらい L が R と結合しやすいかを表す指標として考えることが出来ます。

　ヒル係数が大きいと、シグモイド型の関数の形を取るようになります。つまり、 $[L]$ が $K_d$ に比べて十分小さい場合は、 $\displaystyle p \approx \frac{[L]^n}{K_d}$ によりゆっくりと立ち上がる形となるのですが、 $[L]$ が $K_d$ より十分大きくなると $p \approx 1$ として最終的に1に漸近します。

f:id:cakkby6:20201019230217p:plain — Hillの式： $K_d = 2$ で $n=1, 2, 4$ がそれぞれ水色・青緑・濃緑

Hillの式： $K_d = 2$ で $n=1, 2, 4$ がそれぞれ水色・青緑・濃緑

　また、（n=1の反応で）実際に解離定数を求めたい場合には、以下の競争結合アッセイと呼ばれる方法を用います。

　まず、分子 L を放射性の標識を付けたもの $L_H$ と付けていないもの $L_C$ にわけます。これらを混ぜて配合した溶液で結合・解離を考える時、 $[L_H R]$ は

$\displaystyle \begin{eqnarray} [L_H R] &=& \frac{([L_H]+[L_C])R_{total}}{([L_H]+[L_C])+K_d} \ \frac{[L_H]}{[L_H] + [L_C]}\\ &=& \frac{[L_H]R_{total}}{[L_C]+[L_H]+K_d}\end{eqnarray}$

と表せます。 $R_{total}, [L_H], [L_C]$ は自分で設定した値であり、 $[L_H R]$ は計測して求めることが出来るため、 $[L_H]$ を一定にして $[L_C]$ を増やすようにして実験を行い、 $L_H R$ が全体の半数を占める時の $[L_C]$ を求めれば $K_d$ が求められます。薬学においてアゴニストやアンタゴニストを知るために使えるようです。

ミカエリス-メンテンの式

　単純な酵素反応も分子の結合・解離を発展させて考えることが出来ます。基質 S と酵素 E が結合し、中間体 ES を経て生成物 P と酵素 E になる反応は、

$\displaystyle E + S \ \overset{k_{1}}{\underset{k_{-1}}{\rightleftharpoons}} \ ES \overset{k_2}{\rightarrow} E + P$

$\displaystyle \frac{d [ES]}{dt} = k_1[E][S] - (k_{-1} + k_{2})[ES]$

と書けます。前回扱った速い変数の断熱消去を中間体にも適用できる（定常状態にある）として、

$\displaystyle k_1[E][S] = (k_{-1} + k_{2})[ES] \Rightarrow [ES] = \frac{[E][S]}{K_M}$

ここで、 $\displaystyle K_m = \frac{k_{-1} + k_2}{k_1}$ としました。 $[E_{total}] = [E] + [ES]$ とすると、

$\displaystyle [ES] = \frac{([E_{total}]-[ES])[S]}{K_M} \Rightarrow [ES] = \frac{[E_{total}][S]}{K_M + [S]}$

と求まり、生成物 P が生成する速度は

$\displaystyle \frac{d [P]}{dt} = k_2[ES] = v_{max}\frac{[S]}{K_M + [S]}$

$v_{max} = k_2 [E_{total}]$

として求まります。こうして求まった式は ミカエリス-メンテンの式 と呼ばれ、 $K_M$ はミカエリス-メンテン係数と呼ばれます（同様の議論はHillの式の時でも可能です）。 $v_{max}$ 以降の項は結合・解離の式の形をしているため、これもシグモイド型の関数になります。そして、 $[S] \gg K_M$ のとき $v_{max}$ へ速度が漸近するため、文字通り最大の速度を表すと言えます。

Ultrasensitivity

MWCモデル（アロステリック制御）

　Hillの式はもともと、ヘモグロビンの酸素解離曲線を上手く説明するモデルとして考えられたと言います。ところが、その酸素解離曲線に実際に当てはめてみると、ヒル係数 = 2.8 と整数にならない不思議な値になってしまいます。これでは 2.8 個の酸素が結合した状態という意味不明なものを表すことになってしまいます。

　そこで、Monod, Wyman, Changeux らによって MWC モデル（協奏モデル・対称モデル）というモデルが提唱されました。ヘモグロビン分子が4量体であり、（全体で）T状態とR状態という2状態に遷移できるとして考えるモデルです。

f:id:cakkby6:20201021151836p:plain — MWCモデル：酸素がどの位置に入っているのかは考慮しない。矢印が太いほど反応がその方向に進みやすいとする。

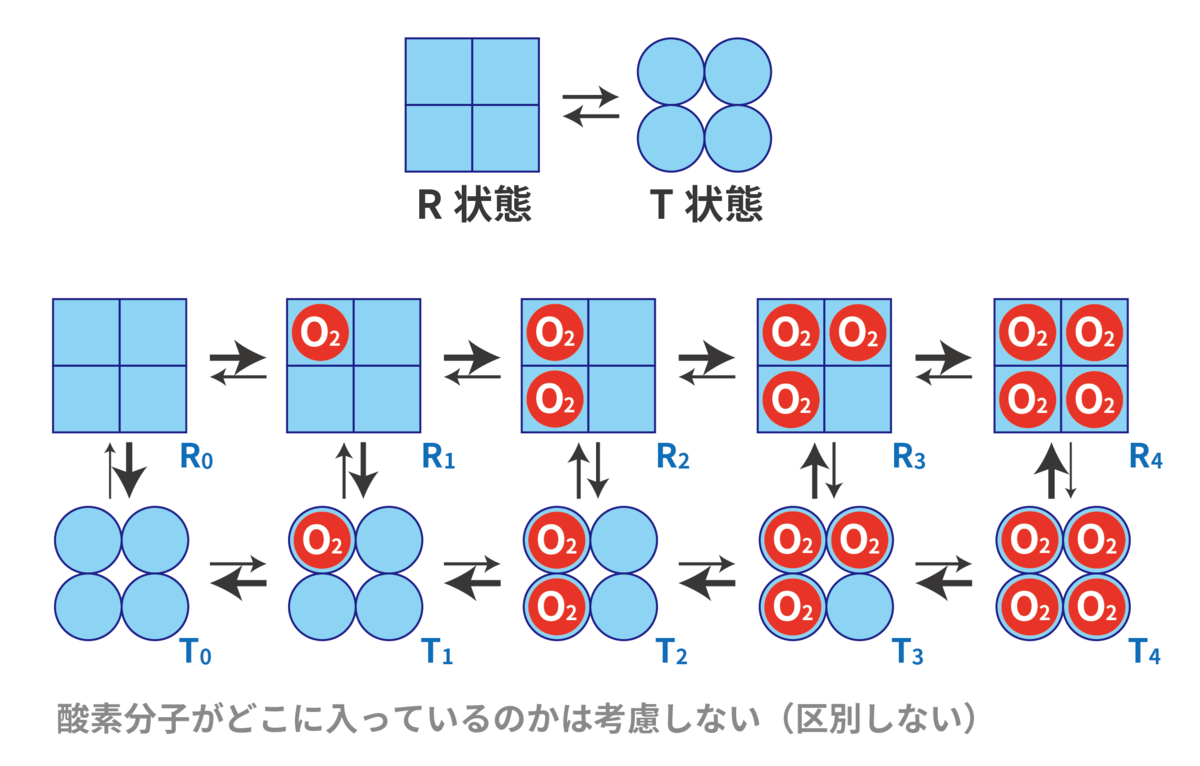
　酸素が $i$ 個ついた2状態をそれぞれ $T_i, R_i$ とすると、ヘモグロビン分子に結合した酸素数 $Y$ は

$\displaystyle Y = \frac{\sum_{i=0}^{4} (i[R_i] + i[T_i])}{\sum_{i=0}^{4}([R_i]+[T_i])}$

となります。T状態とR状態それぞれの1酸素分子との結合反応の平衡定数 $K_T, K_R$ が酸素数 i に依らないとすると、質量作用の法則より

$[T_i] = K_T[O_2][T_{i-1}], [R_i] = K_R[O_2][R_{i-1}]$

となります。また、R状態とT状態の遷移反応の平衡定数を $L_i = \frac{[T_i]}{[R_i]}$ とおきます。全体が平衡状態に達するときは、それぞれの反応がうまく釣りあっている状態（詳細つりあい）だと考えられます。例えば

$\displaystyle \begin{eqnarray} L_1 &=& \frac{[T_1]}{[R_1]} \\ &=& \frac{[T_1]}{[T_0]}\frac{[T_0]}{[R_0]}\frac{[R_0]}{[R_1]} \\ &=& \frac{K_T}{K_R} L_0 \end{eqnarray}$

と書けます。 $L_2, L_3$ についても同様に $L_0$ に比例した形で書けることが分かります。つまり、 $\displaystyle \frac{K_T}{K_R} = c$ とおくことにすると、

$L_i = L_0 c^i$

となります。 $L_i$ を用いて $Y$ を変形すると

$\displaystyle Y = \frac{\sum i[R_i](1+L_i)}{\sum [R_i](1+L_i)}$

となり、 $x = K_R[O_2]$ と置きなおして $[R_i], [L_i]$ を消去すると

$\displaystyle Y = \frac{\sum i {}_4 \mathrm{C}_i x^i[R_0](1+c^i L_0)}{\sum \ {}_4 \mathrm{C}_i x^i [R_0](1+c^i L_0)} = \frac{\sum i {}_4 \mathrm{C}_i \ x^i + L_0 \sum i {}_4 \mathrm{C}_i \ (cx)^i}{\sum \ {}_4 \mathrm{C}_i \ x^i + L_0 \sum {}_4 \mathrm{C}_i \ (cx)^i}$

となります。ここで登場した式の形は、二項係数の性質により

$\displaystyle \sum {}_4 \mathrm{C}_i \ a^i = (1 + a)^4$

$\displaystyle \sum i \ {}_4 \mathrm{C}_i \ a^i = a (1 + a)^{4-1}$

と計算できます。2つ目の式は1つ目の式の両辺を $a$ で微分すればよいです。こうして $Y$ は

$\displaystyle Y = \frac{x (1 + x)^{4-1} + L_0 cx(1 + cx)^{4-1}}{(1 + x)^4 + L_0 (1 + cx)^4}$

と $x = K_R[O_2]$ の関数として求まります。

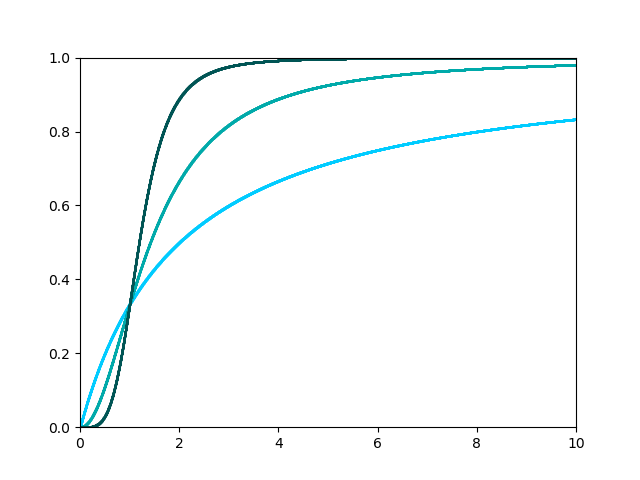
　パラメータ $L_0, c$ を動かしたときにどうなるのかを考えるため、変化させたものをグラフにしました。

f:id:cakkby6:20201021175725p:plain — MWCモデルのパラメータ： $\displaystyle \frac{Y}{4}$ を縦軸 $x$ を横軸にし、左が $L_0$ のみを、右が $c$ のみを変化させたグラフ。下は対数目盛にしたもの。 $L_0 =1000, 100, 10, 1$ の順に色が薄くなっており、 $c = 0.03, 0.3, 3, 30$ の順に緑色が強くなっている。

MWCモデルのパラメータ： $\displaystyle \frac{Y}{4}$ を縦軸 $x$ を横軸にし、左が $L_0$ のみを、右が $c$ のみを変化させたグラフ。下は対数目盛にしたもの。 $L_0 =1000, 100, 10, 1$ の順に色が薄くなっており、 $c = 0.03, 0.3, 3, 30$ の順に緑色が強くなっている。

　水色が実際の酸素解離曲線に近いシグモイド関数のグラフで、そのパラメータは $L_0 \gg 1, c \ll 1$ となっています。これを解析的に考えることも出来ます。例えば $x=0$ 付近での立ち上がりが遅くなるためには、

$\displaystyle \left.\frac{d y}{d x} \right |_{x=0} = 4\frac{L_0 c + 1}{L_0 + 1}$

が 0 に近い値になっていることが必要になります。これは $L_0 \gg 1, c \ll 1$ のときにあたります。また、シグモイド的になるためには、 $x=0$ で下に凸（加速する）関数である必要もあり、条件式として

$(L_0 c^2 + 1) < 4$

が出てきます。

超感度性（Ultrasensitivity）

　MWCモデルではヘモグロビンに合わせて 4量体で考えましたが、上式の流れの 4 を n にそのまま置き換えることで n量体も考えることが出来ます。実際に n を大きくしていきパラメータを調整すると、次のように変化していきます。

f:id:cakkby6:20201021193551p:plain — n量体： $n=4, 8, 16, 32$ の順に色が濃くなっている（縦軸 $\displaystyle \frac{y}{n}$ ）。どんどん急峻になっている。

n量体： $n=4, 8, 16, 32$ の順に色が濃くなっている（縦軸 $\displaystyle \frac{y}{n}$ ）。どんどん急峻になっている。

　nが大きくなると、ある値を境に急に結合の割合が増加するようになっています。このような急激な変化は Hillの式（ミカエリス-メンテンの式も同様）でヒル係数を大きくしたときにもおきます。生物的には、ある状態から次の状態へすぐに変化するような敏感な反応に利用することができ、超感度性（Ultrasensitivity）と呼ばれています。

　超感度性は例えば、誘引物質の有無で大腸菌の進行方向を切り替えることや、細胞分裂のG2期からM期への不可逆的な遷移など幅広い箇所で利用される仕組みです。MWCモデルによって超感度性を再現することができましたが、他の方法でも超感度性の仕組みは作り出せます。

push-pull型反応と zero-order Ultrasensitivity

　生体では分子をリン酸化・脱リン酸化することで活性を調整するシグナル伝達の仕組みがあります。今、分子 $R$ は酵素 $E_1$ によってリン酸化され $R^*$ となり、酵素 $E_2$ によって脱リン酸化され $R$ に戻る仕組みを考えます。

$\displaystyle E_1 + R \ \overset{k_{1}}{\underset{k_{-1}}{\rightleftharpoons}} \ R E_1 \overset{k_2}{\rightarrow} E_1 + R^*$

$\displaystyle E_2 + R^* \ \overset{k_{3}}{\underset{k_{-3}}{\rightleftharpoons}} \ R^* E_2 \overset{k_4}{\rightarrow} E_2 + R$

　両方の反応に対してミカエリス-メンテンの式と同様に考えると

$\displaystyle \frac{d [R E_1]}{dt} = E_{1tot}\frac{[R]}{K_{M1} + [R]}$

$\displaystyle \frac{d [R^* E_2]}{dt} = E_{2tot}\frac{[R^*]}{K_{M2} + [R^*]}$

となります。実際にこの反応式を解くのは補足にするとして、定性的に考えてみます。上のミカエリス-メンテンの式では、過剰量の基質が存在する場合、ほぼ基質の濃度に依らず最大速度近くの勢いで反応が進行します。両者とも最大速度近くの勢いで反応する状況を考えてみると、十分時間がたった後では少しでも速度が大きい反応の方が多く進行し、生成物が偏っていると想像できます。

　すなわち、 $K_{M1}, K_{M2} \ll 1$ かつ $\displaystyle \kappa = \frac{K_{M1}}{K_{M2}} = 1$ という状態にて、定常状態での $R^*$ の量は

$V_1 = v_{1max} = k_2 E_{1tot}, V_2 = v_{2max} = k_4 E_{2tot}$

の比 $\displaystyle x = \frac{V_1}{V_2}$

によって大きく変化すると考えられます。実際、 $K_2$ をどんどん小さくする（反応がすぐに進むようにする）と、超感度性が現れるようになります。

f:id:cakkby6:20201021203153p:plain — push-pull型のUltrasensitivity： $K_2 (= K_1) = 1, 0.1, 0.01$ の順に色が濃くなっている

push-pull型のUltrasensitivity： $K_2 (= K_1) = 1, 0.1, 0.01$ の順に色が濃くなっている

　この反応は、 $R^*$ へと push する反応と $R$ へ pull する反応を組み合わせた push-pull型 と呼ばれています。そして、基質が酵素に比べて過剰に存在する場合に、反応速度がほぼ一定になる（ゼロ次）ときに超感度性を示すため、 zero-order Ultrasensitivity と呼ばれています。

多重リン酸化

　他にも、リン酸化を複数組み合わせることで超感度性を示す場合もあります。例えば、リン酸化された分子 $X^*$ が分子 $Y$ をリン酸化し $Y^*$ とします。その $Y^*$ が今度は、分子 $Z$ をリン酸化し $Z^*$ とします（それぞれの分子の総量は 1 に規格化することにします）。このような反応の定常状態も、ミカエリス-メンテンの式によって

$\displaystyle [Y^*] = \frac{[X^*]^n}{K_X + [X^*]^n}$

$\displaystyle [Z^*] = \frac{[Y^*]^m}{K_Y + [Y^*]^m}$

と書けます（ヒル係数をそれぞれ $n, m$ として）。

　 $m = 1$ のときを考えてみます。単純に上の式を組み合わせれば

$\displaystyle [Z^*] = \frac{\frac{[X^*]^n}{K_X + [X^*]^n}}{K_Y + \frac{[X^*]^n}{K_X + [X^*]^n}} = \frac{[X^*]^n}{(K_Y + 1)(\frac{K_X K_Y}{K_Y + 1} + [X^*]^n)}$

と書けます。これもミカエリス-メンテンの式の形を成しており、その係数部分は $\displaystyle \frac{K_X K_Y}{K_Y + 1}$ となっています。もし $K_Y < 1$ ならば係数部分は小さくなるため、グラフ全体が左に動く形になります。

f:id:cakkby6:20201021212453p:plain — 多重リン酸化 m=1：水色が $Y^*$ 青緑色が $Z^*$ で、左にシフトしている（n=1）

多重リン酸化 m=1：水色が $Y^*$ 青緑色が $Z^*$ で、左にシフトしている（n=1）

　多重リン酸化によって複数の分子を媒介して情報を伝達する流れは、カスケードと呼ばれています（滝のアナロジー）。この場合、カスケードが下のものほど上流の分子の量が少なくても応答するようになるという風に定性的に解釈が出来ます。

　 $m > 1$ の場合、先ほどのようにきれいな式の形にすることは出来ませんが、近似的に考えることは出来ます。 $X^*$ の量が多くない場合は、ミカエリス-メンテンのグラフの左端のように、

$\displaystyle [Y^*] \approx \frac{[X^*]}{K_X}$

考えて問題がないため、

$\displaystyle [Z^*] \approx \frac{[X^*]^{mn}}{K_Y + [X^*]^{mn}}$

となります。つまり、係数部分の値はほぼ同じですが、ヒル係数部分が m×n として上昇し、超感度性が生じることになります。

f:id:cakkby6:20201021213629p:plain — 多重リン酸化 m>1：先ほどと異なり、急峻な形になる（対数スケール）

入出力と回路

フィードバックスイッチ

　push-pull型の反応では zero-order の Ultrasensitivity について考えましたが、ここでは通常の状況を考えてみます。pushする反応の酵素を $S$ 、pullする反応の酵素を $I$ とすると、

$\displaystyle R \ \overset{k_{1}}{\underset{k_{-1}}{\rightleftharpoons}} \ R^*$

$\displaystyle \frac{d R^*}{dt} = k_{1} S (R_{tot} - R^*) - k_{-1} R^*$

定常状態では

$k_{1} S (R_{tot} - R^*) = k_{-1} R^*$

と考えられます。ここで、左辺を $g(R^*)$ 、右辺を $f(R^*)$ とおくことにします。左辺は $R^*$ を増加させる反応部分に、右辺は減少させる反応部分に対応していることになります。このとき、 $\displaystyle p = \frac{R^*}{R_{tot}}$ を横軸にとり、 $g(R^*), f(R^*)$ の値を縦軸に取ったグラフを考えてみると、次のようになります。

f:id:cakkby6:20201029191708p:plain — push-pull型： $S=1.5, k_1 = k_{-1} = 1$ とし、ピンク色が $g(R^*)$ 、水色が $f(R^*)$ に対応。交点が固定点であり、図から安定であることが分かる。

push-pull型： $S=1.5, k_1 = k_{-1} = 1$ とし、ピンク色が $g(R^*)$ 、水色が $f(R^*)$ に対応。交点が固定点であり、図から安定であることが分かる。

　Ultrasensitivityの場合は基質がかなり多い（傾きが急）ときであり、固定点になる比率 $p$ が大きく動くことが分かります。

　次に、このpush-pull型反応のモデルにおいて、 $R^*$ が $S$ の反応を促進するような状況を考えます。 $R^*$ が増えるほど $S$ を活性化するようなモデルであり、ポジティブフィードバックと呼ばれます。フィードバックは得られる結果が過程部分に戻ってくることで、促進する方向に働くためにポジティブとつきます。

　まずは、 $R^*$ に対して線形的にフィードバックされる系を考えます。

$\displaystyle \frac{d R^*}{dt} = k_{1} S (R_{tot} - R^*) + k_{2} R^* (R_{tot} - R^*) - k_{-1} R^*$

定常状態は

$(k_1 S + k_2 R^*)(R_{tot} - R^*) = k_{-1} R^*$

となります。これも左辺と右辺を $g(R^*) , f(R^*)$ とおき、例のグラフにすると以下のようになります。

f:id:cakkby6:20201029194204p:plain — 線形ポジティブフィードバック： $S=0, k_1=k_{-1}=1, k_2=4$ 固定点が2つあり、 $p=0$ のものは不安定で、もう片方は安定。

線形ポジティブフィードバック： $S=0, k_1=k_{-1}=1, k_2=4$ 固定点が2つあり、 $p=0$ のものは不安定で、もう片方は安定。

　 $g(R^*)$ が複雑になったことで、固定点の数が増加しました。次はもう少し複雑なフィードバック機構について考えます。

双安定とヒステリシス

　先のポジティブフィードバックは線形なものでしたが、今度はHillの式で表されるようなシグモイド関数型で考えてみます。 $R^*$ の多量体のようなもので反応が促進されるような何らかの仕組みに相当します。

$\displaystyle \frac{d R^*}{dt} = k_{1} S (R_{tot} - R^*) + k_{2} \frac{(R^*)^n}{K^n + (R^*)^n}(R_{tot} - R^*) - k_{-1} R^*$

定常状態は

$\displaystyle (k_{1} S + k_{2} \frac{(R^*)^n}{K^n + (R^*)^n})(R_{tot} - R^*) = k_{-1} R^*$

と考えられます。 $n=4$ （ヒル係数4）での反応は以下のようなグラフの状況になります。

f:id:cakkby6:20201029201116p:plain — シグモイド型ポジティブフィードバック： $k_1 = k_{-1} = 1, k_2 = 7, K=0.1$ とし、 $S$ の値が大きくなるほど色が濃くなっている（ $S$ は y切片と同じ値）。途中で固定点の数が変化している。

シグモイド型ポジティブフィードバック： $k_1 = k_{-1} = 1, k_2 = 7, K=0.1$ とし、 $S$ の値が大きくなるほど色が濃くなっている（ $S$ は y切片と同じ値）。途中で固定点の数が変化している。

　 $S=0$ では固定点の数が3つ存在し（それぞれ固定点 1, 2, 3 と名付ける）、固定点 1, 3 は安定、固定点 2 は不安定だと分かります。この時、初期の $p$ の値が固定点 2 に相当する $p$ より大きい場合と小さい場合で最終的に行きつく固定点が 1 か 3 のどちらかになる、双安定な状況だと分かります。前回の記事にあったように、スイッチ的な機構に使えることが分かります。

　そして $S$ が大きくなるにつれて、固定点 1, 2 が近づいていき、途中で両者が対消滅することになります。つまり固定点 1, 2 はサドルノード分岐に相当し、一定量以上の $S$ では固定点 3 のみが安定な状況にシフトします。分岐の様子を図にすると次のようになります。

f:id:cakkby6:20201029202046p:plain — ヒステリシス：下二つがサドルノードになっており、途中で対消滅した（都合でその瞬間までは書かれていない）のち、固定点 3 のみが残っている様子。

　ここで、最初 $S$ の量が少ない状況から多くしていった場合、固定点 1 にいた状態は途中で固定点 3 にシフトすることになります。一方、多い状況から少なくしていった場合には、固定点 3 にいた状態は $S=0$ になるまでずっと安定な固定点 3 に居続けることになります。すなわち、安定な状態の遷移変化が以前の状態に依存します。このような過去の「履歴」に依存する現象をヒステリシスと呼びます。この系はヒステリシスの一例で、（細胞周期のような）不可逆的なスイッチの仕組みに応用されています。なお、”トグル・スイッチ”は可逆的なので対になる概念だと言えます。

フィードフォワード回路

　フィードバックの反対に、結果がさらなる反応の結果に影響を及ぼすような場合を、フィードフォワードといいます。

　ここでは、次のモデルを考えます。分子 $X$ は分子 $Y$ を増加させ、分子 $Y$ は分子 $Z$ の増加を抑制します。一方、 $X$ は分子 $Z$ を増加させます。また、各分子は一定時間で同じように分解も進むものとします。すると、それぞれの反応は次の式にまとめられます。

$\displaystyle \frac{d Y}{dt} = -\gamma (Y - A(X))$

$\displaystyle \frac{d Z}{dt} = -\gamma (Z - G(X, Y))$

ここで、 $\gamma$ は時間ごとの分解の定数で、 $A, G$ は各分子の量の増加に関する関数です。例えば $A(X)$ は $Y$ が $X$ によって増加する量を表していると考えられます。実際にこの部分がどのような関数で表されるのかについては、酵素反応の活性化・抑制についての式をミカエリス-メンテンの式について考える必要があります。

　ミカエリス-メンテン式において、活性化した反応の形はおよそ元の式と同じであり、比例定数の部分で近似して考えることが出来ます。つまり

$\displaystyle \frac{d [P]}{dt} = V\frac{S^n}{K^n + S^n}$

の形で書けます。一方、抑制する反応、特に今回のようなアロステリックな抑制反応は変わってきます。生成物の量は酵素反応の中間体に比例していました。今、 $S, E$ の反応を $I$ が非競争的に阻害するとすると、 $I$ の反応は結局結合解離の式に落とし込めるため、結合する割合は

$\displaystyle \frac{I}{K_d + I}$

の形で書けます。酵素はこのどちらかに割り振られるようになるため、阻害される反応の中間体は「阻害剤の結合ではない割合×普通の酵素反応の式」の形で書けると言えます。すなわち、

$\displaystyle [ES] =(1 - \frac{I}{K_d + I})\frac{[S]}{K_M + [S]} = V \frac{K_d}{K_d + I}$

となります。一般的にも、抑制する反応は

$\displaystyle \frac{d [P]}{dt} = V\frac{K^n}{K^n + I^n}$

の形で書けるといいます。実際、この式は $I$ が多いほど $P$ が少なくなっていく（抑制されていく）ことを表せています。

　本題のフィードフォワード回路に戻って考えます。一般の活性化・抑制の式により、 $A(X)$ は

$A(X) = V\frac{X^n}{K^n + X^n}$

の形であると分かります。一方の $G(X, Y)$ は「Yからの抑制とXからの促進」の組み合わさった関数であると考えられます。この式の形は、先ほど求めたアロステリック阻害の式の形から考えることが出来ます。あの式は通常の酵素反応の式と抑制の式の積の形で書けていましたが、今「Xからの促進」を通常の酵素の反応式の促進の形と同じものと考えても問題ないため、 $G(X, Y)$ は「促進×抑制」の形であると考えられます。実際、その状況を図にすると次のようになります。

f:id:cakkby6:20201029220111p:plain — フィードフォワード回路：ピンクが促進、青が抑制、緑が $G(X, Y)$ で積（AND）の形をしている（横軸は対数軸）。

フィードフォワード回路：ピンクが促進、青が抑制、緑が $G(X, Y)$ で積（AND）の形をしている（横軸は対数軸）。

　このように回路システムの応答は積（AND）を用いて多段に重ねることが出来ます。これらは、例えばショウジョウバエの発生に重要なモルフォジェンと最終的な体節などの構造との関連の解析に応用されているようです。

　今回はこれで終わりです。次回は定常状態以外の振動などの現象・神経回路のシミュレーションなどについて扱います。