もし生物情報科学専攻の大学院生が "StableDiffusion" を理解しようとしたら 8 ~Stable Diffusion①~

前回

cake-by-the-river.hatenablog.jp

今回は、いよいよStable Diffusionの元論文である Latent Diffusion Model (LDM) について解説し始めます。特に、そのモデル構造（潜在空間における拡散モデル, 分類器なし条件付け, など）を導くに至った経緯を主に解説します。その他の問題（拡散ステップ数の削減など）に関しては次回になると思います。

arxiv.org

Latent Diffusion Model

DDPMとRate-Distortion理論

前回解説したDDPMなど拡散モデルは、入力画像を少しずつガウスノイズへと変換し、そのガウスノイズを少しずつデノイジングし元画像を復元するAutoEncoderでした。これをまた新しい観点で捉えなおすことで、情報理論という分野の知見を得ることが出来ます。

情報理論とは、文章や画像・音声などがもつ情報、あるいはそれを伝達する際に生じる現象について論ずる学問分野と言えます。特に、情報伝達に関する理論について、ここでは考えていくこととします。

例えば、画像をコンピュータAからコンピュータBへと移すことを考えてみましょう。デジタル画像も結局は数字などの文字によって情報が並べられた文章（文字列）であるため、画像全体を表す文字列をAからBへと送信することになります。しかし、これでは通信環境によって内容が一部欠けたり、大きな画像では通信する量が増え、通信料がかさむかもしれません。

そこで、画像の中にある情報を上手く保持しながら、送る文字列の長さ（ここでは「全体の符号長」と呼ぶことにします）を抑えられないか考えてみましょう。簡単な方法としては、最もよく出てくる数字を改めて長さの短い文字へと割りふり、あまり出てこない数字は長めの文字を割り当てることが考えられます。例えば白い背景の画像を主に送る場合、白色のRGB=(255,255,255)では255という3文字が頻出するわけですが、これに 0 を改めて割り振れば (0,0,0)と短くなり、全体の符号長を抑えることが出来そうです。他にもあらゆる方法で情報を圧縮できそうです。

さて、この仕組みを少し抽象的に捉え、数学的な問題にしてみましょう。

コンピュータAはとある分布 $q(x)$ に従うデータ $x$ を可能な限り圧縮してコンピュータBへと送りたいと考えています。そこで、何かしらデータを圧縮できる機械（符号器と呼ばれます）にかけて、圧縮された表現 $z$ を得たのち、コンピュータBへと送ります。コンピュータBはAから送られてきた $z$ を元のデータに戻せる機械（復号器と呼ばれます）に入れ、復元されたデータ $\tilde{x}$ を手に入れます。

このとき、 $D$ 個分の元データと復元された画像の誤差の平均（正確には二乗平均平方根） $\sqrt{\| x - \tilde{x} \|^2 / D}$ は、復元しきれなかった情報を表し、この過程で生じた歪み（Distortion）と呼ばれています。一方、元のデータ $x$ を送信するときよりも、圧縮した後の表現 $z$ の方が全体の符号長は短いはずです。これを定量化するため、圧縮後の一文字がもつ符号長を考え、レート（Rate）と呼びます。一般に、圧縮を強くする（レートを下げる）と、復元が困難になり歪みは酷くなる、というトレードオフ関係が成り立ちます（Rate-Distortion理論）。

ところで、符号器と復号器はそれぞれ英語で Encoder と Decoder となりますが、見覚えはないでしょうか。そうです、AutoEncoderなどで登場するあのニューラルネットワークは、この情報理論の文脈が由来となっています。VAEや拡散モデルはAutoEncoderとして考えることができ、拡散モデルでは拡散過程が符号器、逆拡散過程が復号器となります。そこで、今説明したレートと歪みの関係を、DDPMに当てはめてみましょう。

DDPMの時刻 $t=T, T-1, ..., 1, 0$ の潜在変数 $x_t$ について、逆拡散過程 $p_\theta(x_t | x_{t+1})$ を用いてサンプリングを行います。一方、拡散モデルでは各時刻の潜在変数から入力画像を解析的に予測することが出来ました。

$\displaystyle q(x_t | x_0) = \mathcal{N} (x_t; \sqrt{\bar{\alpha_t}} x_0, \bar{\beta_t} \mathbb{I}),\ \ \bar{\alpha_t} = \prod_{s=1}^t \alpha_s,\ \ \bar{\beta_t} = 1 - \bar{\alpha_t}$

これを用いて元画像を推定します（本当はガウス分布ですが、ここでは誤差の計算を楽にするため決定的にしています）。なお、具体的な送受信の構成については、末尾に情報理論との関連も兼ねて追記しています。

$\tilde{x_0} = (x_t - \bar{\beta_t}\epsilon_\theta(x_t)) / \sqrt{\bar{\alpha_t}}$

さて、このようにして元画像を推定する枠組みのもと、レートと歪みの間の関係を示したのが次の図です。

左図は逆拡散過程が進むにつれて元画像が上手く推定できるようになり、歪みが徐々に減少していく様子を表しています。真ん中の図はレートに関する情報で、レートと歪みの関係は右図になります。逆拡散過程に対し緩やかに変化していた歪みと比べて、レートは逆拡散の最終局面まで非常に低い状態で抑えることが出来ており、レート歪み関係も左下へと偏っていることが分かりました。これは何を意味するのでしょうか？

上の結果は、低いレート領域、すなわち画像内にノイズを除いて存在する情報の量が少ない場合（逆拡散過程の初期～中期）でも、デノイジングを進めることで効率的に歪みを抑えることが出来るという解釈が可能です。つまり、実際の画像において、（圧縮によって失われやすい）多くの情報は逆拡散過程の最終局面に集中しているわけです。この考察が Stable Diffusion で採用されている Latent Diffusion Model（LDM） の発想につながります。

潜在空間での拡散モデル

Rombachたちは、レートと歪みの関係について、DDPMにおける分析の結果、二つの圧縮プロセスに分離できると考えました。

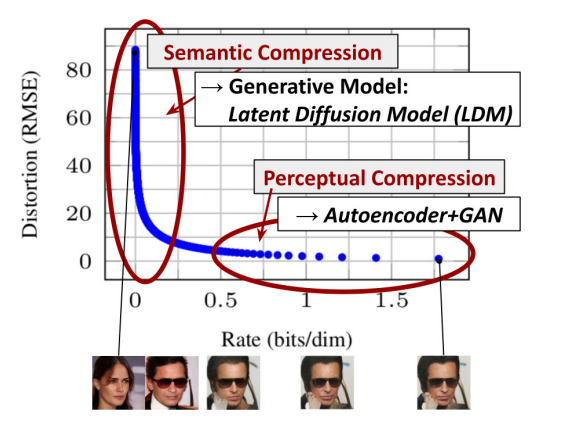
画像の圧縮フェーズの分離。歪みが大きい部分は意味的圧縮、レートの大きい部分は認識的圧縮としている。LDM論文より引用。

各レートにおける画像の例を見ると分かるように、低いレートの領域での復元画像は、拡散過程の変化に伴い内容自体がダイナミックに変化しており、そもそも画像の持つ意味をよく表す領域（意味的圧縮, Semantic Compression）だと言えます。一方、高レート領域の復元画像の多くは似通っており、意味的圧縮で得られた情報を実際の画像へと昇華するプロセス（認識的圧縮, Perceptual Compression）に対応すると考えられます。

一方で、拡散モデルは画像自体にノイズを加えるモデルであり、高画質の画像を生成しようとすると、非常にリソースを食うことが知られていました。そのため、出来る限りリソースが抑えられる小さな空間での拡散を行った方が良いと言えます。

そこでStable Diffusionでは、低いレート、すなわち持っている情報の量は抑えられる意味的圧縮に拡散モデルを用い、認識的圧縮部分には高画質な画像生成を得意とするVAEなどのAutoEncoderモデルを用いる2ステージ型のモデルを採用しました。これにより、高画質な画像を生成するという目標は残しつつ、リソースは抑えられます。

更に、このアプローチの良い点として、AutoEncoder部分の学習を分離し、汎用な高画質生成パートとして使いまわせるようにできることが挙げられます。このことは、とくに意味的圧縮部分において、文章や周囲の画像による条件付けを行った場合（後述）でも、全体の学習をし直す必要がないという意味で非常に使い勝手がよくなると言えます。

これらを踏まえたうえでLDMの全体概略図を見てみましょう。

左上の入力画像 $x$ は、まずVAEのEncoder $\mathcal{E}$ により潜在変数 $z$ へと変形されます。潜在変数内では拡散過程によりガウス分布へと変遷し、逆拡散過程により再びもとの潜在変数へと戻るモデルを考えます。デノイジングを行う部分ではU-Net型の構造を主に利用し、条件付け（Conditioning, 後述）を可能にするため、Attention機構を用いています。この辺りは後ほど説明します。

VAEによる高品質画像生成

まずは理解しやすいVAE部分（Encoder, Decoder）を見てみましょう。なお、以降では第2,3回で説明した内容が出てくるので、覚えていない！という方は少し見返してみると幸せになれるかもしれません。

cake-by-the-river.hatenablog.jp
cake-by-the-river.hatenablog.jp

Stable Diffusionでは、Encoderによって画像の空間をより小さな潜在変数 $z$ へと圧縮するのでした。ずいぶんと前の回で、同じEncoder-Decoder型の構造をとり、情報を圧縮する具体的なネットワークとしてU-Netを紹介しましたが、このEncoderでもそれと似た構造を採用します。すなわち、畳み込み（Conv2d）を用いて画像を圧縮し、逆畳み込みで拡大します。このとき、スキップ接続（残差ブロック, ResBlock）を利用することで、深いネットワークの学習の困難も減り、精度が向上します。ただし、U-NetではEncoder-Decoder間でのスキップ接続を行っていましたが、ここでは各々の内部で利用するにとどめていることに気を付けます。

実際に使われるEncoderのアーキテクチャの例を示しました。主にDownフェーズとMiddleフェーズに分解され、それぞれでResBlockを多用します。ResBlock内では2回分の畳み込み（doubleConv）を元入力に加えるようにしており、Downフェーズでは、何回かResBlockを嚙ませて（上図では1回のみ）から、ダウンサンプリング＆チャネル数の増加を行っています。

一方、Middleフェーズでは、ResBlockの間に、畳み込み層の結果をQ,K,VとしたSelf-Attention（入力が）を導入したAttentionBlockが存在します（なぜこの層を挟んだのかは不明ですが、おそらく後ほど扱う拡散モデルの構造との類似が関係しそうです）。

また、各層で随時Group Normalization（Batch Normalizationの進化版）を導入し、ReLUの代わりにSwish（SiLUとも呼ばれる）という微分可能な活性化関数を用いています。この辺りは、U-Netの時のコードと比較すると違いが分かりやすいと思います。

これらはザックリと次のように実装されます（疑似コードなのでかなり簡略化しています）。

doubleConv(in_channels, out_channels) = Sequential(
    GroupNorm(out_channels), Swish(),
    Conv2d(in_channels, out_channels, kernel_size=3, padding=1),
    GroupNorm(out_channels), Swish(),
    Conv2d(out_channels, out_channels, kernel_size=3, padding=1)
)

ResBlock(in_channel) = x + doubleConv(in_channel, in_channel)(x)

Encoder = Sequential(
    # Down phase
    Conv2d(c: 3 -> 128),
    for level:
        for block:
            ResBlock,
        Conv2d, # ダウンサンプリング
    # Middle phase
    ResBlock,
    AttentionBlock,
    ResBlock,
    Conv2d(c: 512 -> 4×2)
)

この場合、Encoderの出力は縦横 64×64 でチャネル数 8 の画像の形式をしています。ただし、実際にはこのチャネルを2等分し、それぞれ潜在変数 $z$ の平均と標準偏差として扱い、潜在変数 $z$ 自体はこれらに従うガウス分布からのサンプルとして取り扱います。つまり、各潜在変数 $z$ は 64×64 でチャネル数 4 の画像のような形式となっています。

さて、DecoderパートはEncoderの逆を行うこととなります。

なお、必ずしもEncoderと同じアーキテクチャにする必要はなく、ResBlockの数を増やしたり拡大・縮小の層数を変えることもあります。

せっかくなので実際の動きを見てみます。今回用いたVAEは 512×512 の大きさで学習されています（Stable Diffusion ver 2.0 では 768×768 となりました）が、入力画像は必ずしもこのサイズである必要はありません（CNNなど畳み込み系の特徴）。また、画像の各ピクセルの値は普通 $[0, 255$ ] の範囲で示されますが、入力する際には、 $[-1, 1$ ] の範囲に変形させます（Decoderの出力は逆変換を行う）。

潜在変数である $z$ の各チャネルごとの傾向はモデルごとに異なるとは思いますが、元が（カーネルの小さな）畳み込みネットワークであることからもわかるように、基本的に画像全体の傾向は保存されるようです。

さらに、よく画像を観察すると復元画像は一部元画像と異なる部分があります。特に、目のグラデーションや色味（鮮やかさ）は変わっているようで、VAEの学習の質によってこれらの要素が変化しうることが分かります。

また、今回は割愛してしまうのですが、ベクトル量子化（複数のベクトルをある代表的なベクトルで置き換え、離散化すること）を用いた VAE （VQ-VAE）を用いることもできます。いずれの場合でも、潜在変数に可能な限り歪みなく情報を圧縮し、復元可能にすることがこのパートでは重要だと言えます。

Conditioning

いよいよ、モデルの中枢となる拡散モデル部分に移ります。ただし、今までと異なり、ここには条件付け（Conditioning）という特殊な機構を導入することとなります。

分類器なしガイダンス（CFG）

私たちは、NCSNの記事以来、とにかく画像を自然に上手く生成する方法のみに着目してきました。しかし、実際に欲しいのは「青空の下咲き乱れるひまわりの畑の写真」といった条件を反映した画像の生成です。これらは条件付け画像生成と呼べます。そして、条件 $y$ のもとで画像 $x$ が生み出される確率 $p(x|y)$ を求める問題として考えることが出来ます。この確率はベイズの定理を用いると

$p(x|y) = \frac{p(y|x)p(x)}{p(y)}$

と書けます。スコアは $x$ に関する勾配なので

$\nabla_x \mathrm{log}\ p(x|y) = \nabla_x \mathrm{log}\ p(y|x) + \nabla_x \mathrm{log}\ p(x)$

となり、今まで求めてきた $\nabla_x \mathrm{log}\ p(x)$ に、画像 $x$ を条件として条件 $y$ が得られる確率に対するスコアを加えることで求められることが分かります。

後者は、文章（Promptと呼ばれる）を条件とした画像生成の場合、画像の内容を説明する文章を出力する確率と言え、より一般的に画像を分類する問題と言えます。したがって、分類を行うニューラルネットワーク（分類器, Classifier）を別に学習させ、そのスコアをDDPMの学習アルゴリズムに組み込むことで、条件付き画像生成が出来るようになると考えられます。このような方法は、分類器ガイダンスと呼ばれています。

ただし、実際に学習させるときは分類器部分のスコアには重み $\gamma$ を加えます。この重みはガイダンスと呼ばれています。

$\nabla_x \mathrm{log}\ p_\gamma(x|y) = \gamma \nabla_x \mathrm{log}\ p(y|x) + \nabla_x \mathrm{log}\ p(x)$

この処理は何を意味するのでしょうか？元の確率に関する表記に戻すと、

$\displaystyle p_\gamma(x|y) = \frac{p(y|x)^\gamma p(x)}{Z(y)}$

これは、 $p(y|x)$ がカノニカル分布の形で書けると考えた場合、意味が明確になります。

$\displaystyle p(y|x) \propto \mathrm{exp}(-E(y | x))$

$\displaystyle \begin{eqnarray} p_\gamma(x|y) &=& \frac{\mathrm{exp}(-E(y | x))^\gamma p(x)}{Z(y)} \\ &=& \frac{\mathrm{exp}(-\gamma E(y | x)) p(x)}{Z(y)} \end{eqnarray}$

最後の形は、逆温度 $\gamma = 1 / T$ の時のカノニカル分布の形と等しくなります（導出は末尾の追記で）。つまり、ガイダンスは分類器が学習するエネルギー関数 $E(y|x)$ に従う分子の"温度の逆数"に対応したものであり、エネルギー関数に対する応答の強さを決めます。もし $\gamma$ が大きな値を使う場合は、「低温でのサンプリング」とも捉えられ、より条件を重視した画像生成が出来ると言えます。

一方、この方法にはいくつかの問題があります。まず、デノイジング時のスコアに組み込む場合、時刻 $t$ の情報も含んだ分類器を設計しなければなりません。また、画像生成の精度の指標の多くが分類（AIが作ったのかどうか）で評価されるため、分類器を組み込んだモデルではそれが有利になりやすい可能性が指摘されています。

これらを解決するため、Googleから分類器なしガイダンス（CFG, Classifier-Free Guidance）が提案されました。

arxiv.org

これは、先ほどのスコアの数式に再びベイズの定理を適用することからヒントが得られます。先ほどは条件付き画像生成の確率に用いましたが、今回は逆に分類器に相当する確率 $p(y | x)$ に適用します。

$p(y|x) = \frac{p(x|y)p(y)}{p(x)}$

これを分類器ガイダンスの式に代入します。

$\displaystyle \begin{eqnarray} \nabla_x \mathrm{log}\ p_\gamma(x|y) &=& \gamma \nabla_x \mathrm{log}\ p(y|x) + \nabla_x \mathrm{log}\ p(x) \\ &=& \gamma \nabla_x \mathrm{log}\ p(x|y) + (1 - \gamma) \nabla_x \mathrm{log}\ p(x) \end{eqnarray}$

これは、条件付き画像生成のスコアを、条件なし画像生成との間でガイダンス $\gamma$ により重み付けされた平均の形に書き換えたことになります。そこで、文章などの条件を入力として利用できるようなデノイジングのモデル $\epsilon_\theta(x, y)$ を組み込み、一部を $\epsilon_\theta(x, \phi)$ 、すなわち $y = 0$ の場合として学習・サンプリングすることで、分類器を導入せずに条件付け画像生成が出来るといえます。

この論文では具体的な実装が公開されていないようですが、Dropout（条件 $y$ の入力を確率 $1-\gamma$ で $y=0$ とする）を用いたり、実際のスコアを二つの条件での重み付き平均にする方法が取られます。

GLIDE & text2image

さて、残る問題はどのようにして条件を入力としたデノイジングモデルを実際に組み立てるか、となりました。潜在変数 $z$ は、元の画像の形式とは異なりますが、VAEで見たように、認識的に圧縮されていても、画像自体の特徴は残っていました。したがって、一般に画像に対してよく働くことが知られているU-Net型のアーキテクチャを採用するのが考えられます。

条件 $y$ をこのモデルに組み込む方法の一例として、GLIDEというモデルを見てみます。これは、CFGを拡散モデルに導入し、自由なテキストを入力として画像生成を可能にしたモデルの一つです。

arxiv.org

今の今まであまり明示しませんでしたが、NCSNやDDPMでのデノイジングの過程は、時刻 $t$ 自体によっても条件づけられていると言えます。したがって、条件 $y$ のみならず、時刻も入力としたU-Net構造を作る必要があります。条件のデノイジングへの導入に関して、GLIDEでは、U-Netの各ブロックをResBlockとAttentionBlockの複合から構成し、ResBlockには時刻（と文章）の情報を埋め込んだベクトルを、AttentionBlockには文章の情報を追加の入力として受け入れるようにしています。

ResBlockでは、元の入力 $x$ と埋め込まれた条件 $e_{emb}$ がそれぞれ畳み込み・線形変換などの処理を経たのち足し合わされます。この結果（残差） $h$ を元の入力 $x$ と足すことで、全体としてはスキップ接続を行うわけです。一方AttentionBlockでは、入力 $x$ を畳み込んで作成した $Q, K, V$ に加え、事前にTransformerにより圧縮された条件の表現 $e_{encoder}$ を畳み込んだ $K_e, V_e$ を用意し、 $Q, (K,K_e), (V,V_e)$ の Multi-Head Attention （半Self-Attention？とでも呼べる方法）し、スキップ接続します。とにかく条件を上手くデノイジングの過程に導入するわけです。

後はU-Net同様の構造とし、学習時にDropoutを用いて学習します。これがGLIDEでの条件付けの方法だったのですが、StableDiffusionではここの仕組みが若干異なるものとなっています。なんと、AttentionBlockの代わりに小さなTransformer（Spatial Transformer）を入れます（元のAttentionBlockのままにすることも出来ます）。以上を踏まえて、デノイジング U-Net のアーキテクチャを見てみましょう。

StableDiffusionのデノイジングU-Netのアーキテクチャの例。点線はスキップ接続を表す。緑の箱は時刻の埋め込みで条件付けされたResBlockを、オレンジの箱は文章で条件付けされたSpatialTransformerを表す。

時刻 $x$ は、Sinusoidal Embedding と呼ばれる特殊な変換により、幅320のベクトルにしてから一般的なLinear層で埋め込みます。

一方、条件 $y$ の埋め込みは色々なパターンがあります。文章の場合、以前扱ったCLIPのTransformerによる埋め込み（FrozenCLIPEmbedder）を用います。

全体構造はU-Netと類似し、EncoderとDecoderがそれぞれ12個のパーツからなります。SpatialTransformer は、Transformerの元論文と比較すると分かるように、Decoderパートとほとんど同じであり、最初のブロックがSelf-Attention、二個目がCross-Attentionという形を取っています。ただし、各 $Q, K, V$ が画像に対応したもの（Spatial）となっており、畳み込みによって生成されるところが特徴的だと言えそうです。なお、SpatialTransformerの中のTransformerのブロックは複数回繰り返しても構いません（ここでは1つのみの場合を図示）。

CFGスケールと"Negative Prompt"

こうして学習したデノイジングU-Netを用いて、単なるガウス分布に従うサンプルから文章で条件づけた画像生成（text2image）を行うことが出来ます。サンプリングの過程でも、先ほどのClassifier-Free Guidanceの $\gamma$ を用いることが出来ます。すなわち、条件 $y_c$ があるとき（Condition）の出力結果 $\epsilon_\theta(y_c)$ と、条件なしのとき（Uncondition）の出力結果 $\epsilon_\theta(\phi)$ を

$\epsilon_{\theta, \gamma}(y_c) = \epsilon_\theta(\phi) + \gamma (\epsilon_\theta(y_c) - \epsilon_\theta(\phi))$

として補正し、これを用いてデノイジングを行うわけです。

さて、分類器ガイダンスの時のことを考えると、 $\gamma$ は逆温度に対応し、大きな値（ $\gamma > 1$ など）は低温でのサンプリングに対応するということを説明しました。分類器なしガイダンスにおいてはあまり想像しにくいですが、上の式は、条件なしの画像生成に対し、条件ありの結果を $\gamma$ だけ強調するものと言えます。StableDiffusionでは、この $\gamma$ を CFGスケール などと呼びます。

CFGスケールの大きな画像生成は、条件 $y_c$ を重視するとともに、条件なしの生成から離れるような効果を持つことになります。このことを逆手に取ったのが、いわゆる Negative Prompt という概念です。

今の今まで、条件付き画像生成をベイズの定理に基づいて導出しましたが、ベイズの定理は（とくにベイズ統計学の文脈において）、元ある分布を新しい知識で更新する式として捉えることが出来ます。すなわち、 $x$ に関する事前分布 $p(x)$ に、知識 $y$ を加えた際、改めてこの知識を吸収した事後分布 $p(x | y)$ が

$\displaystyle p(x|y) = \frac{p(y|x)p(x)}{p(y)}$

と書けるという意味です。これまでは事前分布 $p(x)$ を条件なし画像生成 $p(x|\phi)$ として捉えたわけですが、別に条件なしである必要はないわけです。そこで、”条件なし”に対応するような条件 $y_{uc}$ を用いることにしましょう。これはStable Diffusion上で、無条件の条件化（unconditional conditioning）と呼んでいます。

$\displaystyle \epsilon_{\theta, \gamma}(y_c) = \epsilon_\theta(y_{uc}) + \gamma (\epsilon_\theta(y_c) - \epsilon_\theta(y_{uc}))$

条件なしに対応する条件 $y_uc$ は、CFGスケールが大きい場合に離れるような条件であることから、好ましくない方向の画像生成の条件として捉えることができます。したがって、text2imageでは、Negative Prompt という用語で扱われます。経験則となってしまいますが、一般的にCFGスケールは7辺りを用いることが多いですが、この値を低くすれば高温のサンプリング、すなわち条件があまり重視されずもやもやとした画像が生成されやすくなります。一方、7を超えて大きくしていくと、条件に引っ張られすぎて過度に強調した不自然な画像ができやすいようです。詳しくは以下を参照してください。

qiita.com

今回は、Stable Diffusionの基本的なアーキテクチャの解説、および text2image を説明しました。次回は、image2image など文章以外の条件付け、およびサンプリングに関する問題の解決について説明します。

非可逆圧縮としてのDDPM

そのうち書きます。

事前分布を持つカノニカル分布に関して

そのうち書きます。