分子からの群論解説（３）群の表現

今回は、群を行列で表現することについて考えます。行列についてある程度知っている前提で進めることになるので注意してください。

群を行列で表現したい

群は「動き」の集まりであって、群の作用の対象は、回転や鏡映を取られるなどします。こうした操作は線形変換とも呼ばれ、行列によって表現することも可能でした。それならば、群の元を自然な形で行列と対応させてみることで、その行列の持つ特徴が群の性質に対応したものとなる気がしてきます。そうすれば、群をベクトルなどの線形代数の世界に落とし込んで具体的に考えることが出来そうです。

それでは、具体的に行列で操作を表現するよう考えてみます。とりあえず、 $C_{3v}$ を行列で表すことにしましょう。

前回の図2aのような平面で考えます。下図3aのように基底ベクトル $(e_1, e_2)$ を取ってみて、 $C_{3v}$ の元によって基底がどこへ移されるかを考えます。図3aでは $C_3, \sigma_1, \sigma_2$ を例に示しています。
f:id:cakkby6:20200214234932p:plain

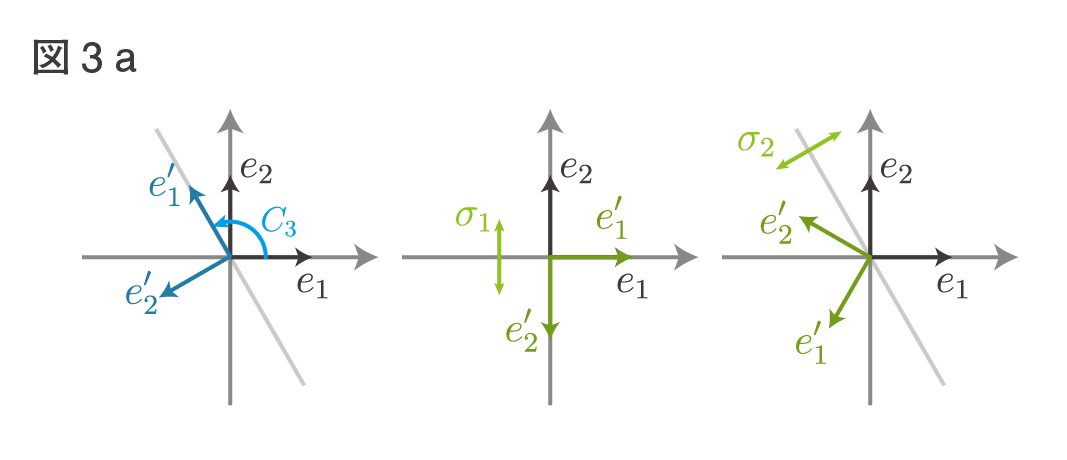
これらの操作に対応した行列はどのように表すでしょうか？移動後の基底と移動前の基底との線形変換を表す行列は表現行列と呼ばれていて、次のような形式で表すことが出来るのでした。

表現行列を $D$ とし、基底（列ベクトルの形式）を行ベクトルのように横に並べたものを $(e_1 \ e_2)$ と表すことにした時
$(e_1' \ e_2') = (e_1 \ e_2)D$

これは
$e_1' = D_{11}e_1 + D_{21}e_2$
$e_2' = D_{12}e_1 + D_{22}e_2$
と具体的に計算することが出来て、変換後の基底を変換前の基底の線形結合で表すようにしたときの係数が、行列に対応する様子を簡潔に表すものでした。

これに沿って $C_3, \sigma_1, \sigma_2$ の表現行列を $D(C_3), D(\sigma_1), D(\sigma_2)$ として計算すると

$D(C_3) = \begin{pmatrix} {-\frac{1}{2}} & {-\frac{\sqrt{3}}{2}} \\ {\frac{\sqrt{3}}{2}} & {-\frac{1}{2}} \end{pmatrix}$

$D(\sigma_1) = \begin{pmatrix} {1} & {0} \\ {0} & {-1} \end{pmatrix}$

$D(\sigma_2) = \begin{pmatrix} {-\frac{1}{2}} & {-\frac{\sqrt{3}}{2}} \\ {-\frac{\sqrt{3}}{2}} & {\frac{1}{2}} \end{pmatrix}$

これらの、新しい基底へと変換する行列 $D$ を用いると、

$\left( \begin{array}{cc} x\\ y\\ \end{array} \right) = xe_1 + ye_2$
と表されるベクトルが移動した後のベクトルは

$\left( \begin{array}{cc} x'\\ y'\\ \end{array} \right) = x'e_1 + y'e_2 = D\left( \begin{array}{cc} x\\ y\\ \end{array} \right)$

と計算することが出来ます。他の元に関しても同様に表現行列を計算できます。

ところで、2次元平面上の点を表すための基底は、上記の王道のような基底でなくとも可能でした。いわゆる斜交座標のように、 $e_1$ は先程と同じで、 $e_2$ を $e_1$ から120度反時計回りに回転させたものとする組の基底でも、平面上のどんな点も表現することが出来ます。この時、群の表現行列はどのようになるのでしょうか？
f:id:cakkby6:20200215124307p:plain

先ほどの3つに関して同じように表現を計算していくと
$D(C_3)' = \begin{pmatrix} {0} & {-1} \\ {1} & {-1} \end{pmatrix}$

$D(\sigma_1)' = \begin{pmatrix} {1} & {-1} \\ {0} & {-1} \end{pmatrix}$

$D(\sigma_2)' = \begin{pmatrix} {-1} & {0} \\ {-1} & {1} \end{pmatrix}$

先程とはずいぶん違った見た目になりました。ところが、群の作用は本来、座標系の取り方とは関係しない「動き」の結果でした。ということは、その表現行列も座標系の取り方（基底）に依らない何らかの性質を持っているはずですね。基底に依らないならば、基底によって見た目が変わった表現行列（例えば上の $D$ と $D'$ ）も、実は「同じとみなせる」かもしれない。表現行列に対しても、同値関係という観点を導入することが出来そうです。

群の表現と同値

$C_{3v}$ だけでなく、より一般の群について群を行列に自然と対応させることについて考えます。

群 $G = \{g_1, g_2, \dots, g_n\}$ に対し、行列の集合
$\Gamma = \{D(g_1), D(g_2), \dots, D(g_n)\}$
が

$g_k = g_ig_j \Rightarrow D(g_k) = D(g_i)D(g_j)$

を満たすとき、 $\Gamma$ は群 $G$ の（行列）表現と呼びます。

どうしてこんな式？と思ったかもしれません。私たちは群を、できる限り忠実に行列で表したかったのでした。それならば、行列自体も群の構造をそのまま保つものが良いですよね。群は積に関して閉じているという構造が重要でした。表現でも同様に、積に関して閉じている、しかも群の積がちょうど表現の積になっているならば、この行列の集合は群の構造を保っていると言えます。だからこのような式を満たすように決めたのです。

ちなみに、表現は群の構造を保っているので、群の単位元（「何もしない」）には単位行列が対応していますし、逆元には逆行列が対応していることも示せます。そうすると、表現自体も群になっていることが分かりますね。実は、行列の中で逆行列のあるもの（正則行列）の集合も群を形成していて、一般線形群などと呼ばれています。 $C_{3v}$ の表現の集合は、一般線形群の部分群になっていると言えます。

群 $G$ の表現は基底によって様々な見た目に変わります。それらを「同じ群 $G$ の表現」として同値とみなすにはどうすればいいでしょうか？

そもそも、群から表現へ対応付けるときに用いた方法は「基底の動き」でした。変換前の基底から変換後の基底には変換行列（表現行列）で移すことが可能でした。また、これらの表現は一般線形群の部分群として考えることが出来ます。ここで前回の共役による同値関係を考えてみます。ある基底での表現と他の基底での表現が「共役の関係」であることも、共役の定義式と同じように考える、つまり基底を変換した先でも同じ働きをしているか、という視点から説明できそうです。

基底 $e = \{e_1, e_2, \dots, e_n\}$ での表現 $\Gamma$ と、基底 $e' = \{e_1', e_2', \dots ,e_n'\}$ での表現 $\Gamma'$ に対し、 $e$ から $e'$ への変換行列を $T$ として

$^{\forall} g \in G, \ D(g)' = T^{-1} D(g) T$

が成り立つとき、表現 $\Gamma$ と $\Gamma'$ は同値（同型とも）であると言う。

この場合の $T^{-1}DT$ は相似変換とも呼ばれます。共役の操作は実際、相似関係かどうか見ることと同じなので分かりやすいですね。

$C_{3v}$ の表現として先ほど現れた、 $\{e_1, e_2\}$ の場合と $\{e_1', e_2'\}$ の場合の表現も、

$T = \begin{pmatrix} {1} & {-\frac{1}{2}} \\ {0} & {\frac{\sqrt{3}}{2}} \end{pmatrix}$

を利用して同値関係であることを示せます。例えば、 $D(C_3), D(C_3)'$ に関して

$T^{-1}D(C_3)T = \begin{pmatrix} {0} & {-1} \\ {1} & {-1} \end{pmatrix} = D(C_3)'$

と共役関係にあることが分かります。このようにして、たとえ基底が異なっている表現であっても、相似変換による同値を使って同じ群の表現であることを確かめられます。

他のタイプの表現

表現の定義は、積の構造を保つものというだけだったので、 $C_{3v}$ の表現として、次のようなタイプの物も実はOKです。

群の元全部を "1" に対応させる表現 $A_1$
$H_1 = \{E, C_3, C_3^2\}$ には "1" を、 $H_2 = \{\sigma_1, \sigma_2, \sigma_3\}$ には "-1" を対応させる表現 $A_2$

実際、 $A_2$ の表現は前回の青と緑の箱の関係のように行ったり来たりが出来るので、表現としてちゃんと成立しています。 $A_1$ は常に "1" のみをとるため、恒等表現とも呼ばれています。

これらの表現は行列には見えないかもしれないですが、1×1行列としてみれば行列になります。表現の次元を表現内の行列の次元として定義すると、 $C_{3v}$ の表現として今のところ、2次元の表現が1つと、1次元の表現が2つ現れました。これらの表現の関係性、また他のパターンの表現があるのかについては、次回にしたいと思います。

今回は群の表現と同値についてでした。次回は、表現の既約分解について書こうと思います。
cake-by-the-river.hatenablog.jp